Martin Mölder: Usaldusvahemikud ja nende tõlgendamine

Viimase nelja aasta jooksul on avalikus ruumis olnud erakondade toetusnumbritest juttu tunduvalt rohkem kui kunagi varem. Oluliselt on paranenud ka nende kajastuste kvaliteet – näiteks on teadvustatud, et tulemustega seoses võib esineda midagi, mille nimi on statistiline viga – kuid arenguruumi on veel oma jagu. 

Üks ring probleeme on seotud selle sama statistilise vea ning sellest tuletatavate usaldusvahemike mõistmisel. Olgu järgnev meeldetuletuseks neile, kellele meeldib rääkida usaldusvahemikest, kuid kes täpselt (ilmselt osalt ka endale teadvustamata) ei tea, mida need tähendavad või kuidas nendega peaks ümber käima. 

Igas avaliku arvamuse küsitluse tulemuses on peidus juhuslik ehk statistiline viga. Statistiline viga tekib sellest, et oma järelduste tegemiseks koguvad küsitlusfirmad andmeid ainult piiratud arvult üldjoontes juhuslikult valitud inimestelt. Kõiki küsitleda ei ole võimalik, tuleb piirduda heal juhul paari tuhande inimesega. See on valim. Kui need inimesed on teatud põhimõtete alusel juhuslikult valitud, siis nende põhjal tehtavad järeldused peegeldavad keskeltläbi ilma kallutusteta seda, mida uuritav grupp inimesi tervikuna arvab. Kuid juhuslik valim tähendab ka seda, et iga kord kui me midagi uurime, võime juhuslikult eksida. 

See, mida oma andmetes näeme – eeldusel, et valim on koostatud õigesti – on parim oletus selle kohta, mis reaalsuses võib tõsi olla. Kui küsitlustulemused ütlevad, et ühe erakonna toetus on 12.4%, siis see on kõige parem oletus selle kohta, mis nende toetus võiks olla. Me võime küll natuke eksida. Kuid muid andmeid meil ei ole ja iga muu oletus vähem tõene. 

Kui valiksime kohe uue juhusliku valimi, oleksid tulemused natuke erinevad. Ja järgmisega taaskord natuke erinevad. Ja nii edasi. Lihtsalt juhuse tõttu. Selle pärast ei saa isegi perfektselt tehtud küsitluse tulemustes alati 100% kindel olla. Tõde võib olla teatud kaugusel sellest, mida oma andmetes näeme. Õnneks on aga võimalik teada saada, kui palju me eksida võime. Kui valim on koostatud juhuslikkuse põhimõtet järgides, siis on võimalik (tänu matemaatilistele seaduspärasustele) välja arvutada, kui palju me oma tulemustes võime eksida – mis vahemikus tõeline tulemus võib reaalsuses olla. Seda nimetataksegi usaldusvahemikuks. 

Erakondade toetusnumbrite tõlgendamisel unustatakse see võimalus eksida sageli ära või kui seda meelde tuletatakse, siis on ilmne, et seda on mõistetud valesti. Loomulikult on oluline teada, et on olemas selline asi nagu statistiline viga ja usaldusvahemik. Kuid oluline on ka teada, mida täpselt see endast kujutab ja kuidas seda peaks õigesti tõlgendama. Kõige parem on siin seda illustreerida mõne konkreetse näitega. 

Oletame, et Norstati ja Ühiskonnauuringute instituudi erakondade toetuse küsitluses on Isamaa toetusprotsent 7.9%. See on see, mida andmetes on võimalik näha. Kuid selles ei ole võimalik 100% kindel olla. Reaalsuses võib Isamaa toetus sellest mõnevõrra erineda – selle 7.9% ümber on nö usaldusvahemik, milles teatud tõenäosusega (tavapäraselt on selleks 95%) võib tõeline väärtus reaalsuses olla. 

Siinkohal saavad aga kommentaatorite teadmised tavaliselt otsa. Ollakse endale teadvustanud, et selline usaldusvahemik on olemas ja et reaalsuses võib toetusnumber olla selle vahemiku sees. Aga lugu ei lõpe sugugi siin. Sellel usaldusvahemikul on teatud omadused, mida tõlgendamisel ja toetusprotsentide võrdlemisel tuleb arvesse võtta.

Tuleb meeles pidada kahte asja – esiteks, usaldusvahemiku ulatus sõltub nii valimi suurusest kui ka sellest protsendist, mida me vaatame ja teiseks, tõenäosus selle vahemiku sees ei ole ühtlaselt jaotunud. 

Mida rohkem on andmeid, seda enam saame oma tulemustes kindlad olla ning seda kitsam on see usaldusvahemik. Seda üldiselt isegi teadvustatakse. Kuid teadvustamata jääb see, et mida lähemal me oleme kas 0%-le või 100%-le, seda kitsam see usaldusvahemik on valimi suurusest olenemata. 

Järgmine joonis näitab meile, milline on 95% usaldusvahemiku ulatus kõikide võimalike protsentide lõikes nelja valimi suuruse – 500, 1000, 2000, ja 4000 – puhul.

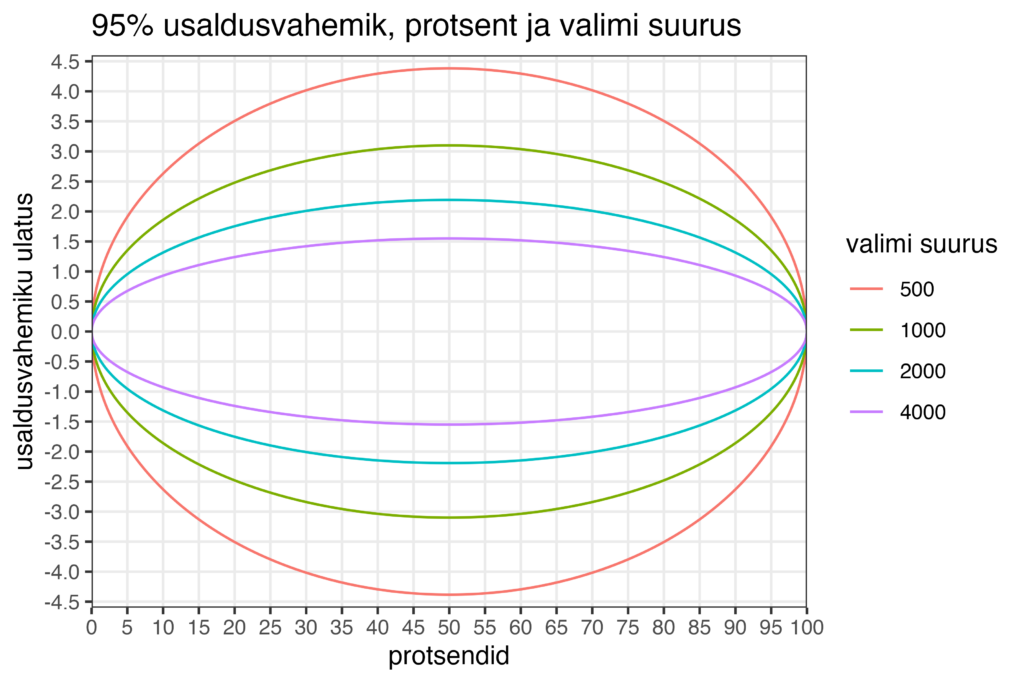
Mida suurem on valim, seda kitsam on usaldusvahemik, sest mida rohkem on andmeid, seda kindlamad saame oma tulemustes olla. See on selge (loodetavasti). Sama valimi suuruse puhul sõltub aga usaldusvahemiku ulatus sellest, mis protsenti me parajasti vaatame. Olenemata valimi suurusest on usaldusvahemikud kõige suuremad 50% puhul – 500 küsitletud inimese puhul näiteks peaaegu +/- 4.5%. Kuid mida väiksemaid või suuremaid protsente me vaatame, seda kitsamaks usaldusvahemikud lähevad. Näiteks kui toetusprotsendiks on 5%, siis 500 valimi puhul on selle 95% usaldusvahemik umbes +/- 2% ehk siis kolmest protsendist seitsme protsendini. Mitte +/- 4.5%. Kui tegeleme suuremate valimitega (2000 või 4000), siis kuskil 10% ja 15% vahemikku jäävate protsentide puhul on see usaldusvahemik kuskil +/- 1% kuni +/- 1.5% kandis. See ei ole just väga suur eksimise ulatus. 

Norstati erakondade toetuse küsitluste valimi suurus on 4000 inimest. Erakondade suhtelise toetuse arvutamisel arvestatakse sellest maha eelistuseta valijate hulk. See tähendab, et valim, millest lõplikud protsendid arvutatakse, on mõnevõrra väiksem. Kui eelistuseta valijate osakaal on kõrge, näiteks 45%, siis jääb sellest 4000-st alles 2200. Kui mõne erakonna toetusprotsent on näiteks 7.9%, siis tähendab see usaldusvahemikku +/- 1.13% ehk siis 6.77% kuni 9.03%. Maksimaalne eksimise määr nii suure valimi puhul (kui erakonna toetusprotsent oleks 50%) oleks +/- 2.09%

Teadlikumad poliitikakommenteerijad on endale praeguseks selgeks teinud, et selline usaldusvahemik erakondade toetusnumbrite ümber on olemas. Kuid peaaegu alati unustatakse ära üks väga oluline detail selle kohta. Tõenäosus selle vahemiku sees ei ole ühtlaselt jaotunud – mida lähemale jõuame usaldusvahemiku piirideni, seda ebatõenäolisem on, et tegelik toetusprotsent on just seal. Ning kõige suurem on tõenäosus selle vahemiku keskel – just seal, kus on see toetusnumber, mida me küsitlusest näeme. See arv, mida andmetes näeme, on igal juhul kõige parem oletus selle kohta, mis päriselt on tõene. Muud informatsiooni (ehk teist või kolmandat samal hetkel tehtud samaväärset juhuvalimit) meil reaalsuse kohta ei ole. Iga teine number selle usaldusvahemiku sees on vähem tõenäoline. Visuaalselt võiks seda tõenäosuse jaotust 95% usaldusvahemiku sees kuvada niimoodi. 

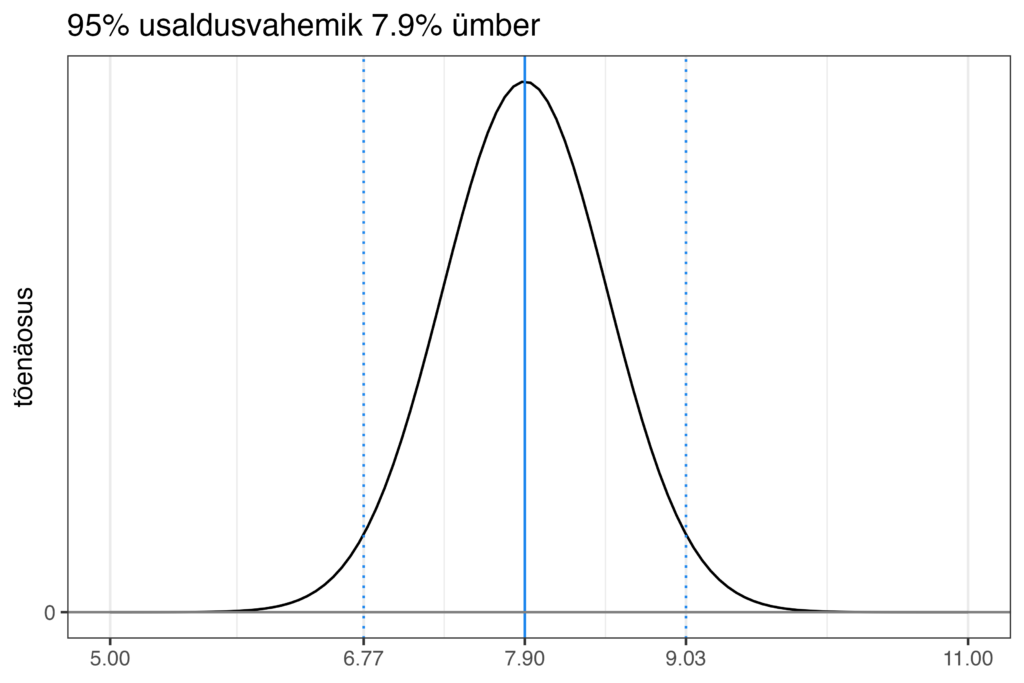
Kaare kõrgus sellel joonisel tähistab tõenäosust. Kui toetusprotsent, mida andmetes näeme, on 7.9%, siis kõige parem oletus selle kohta, mis reaalsuses võiks tõsi olla, on ikka see sama 7.9%. Mida kaugemale sellest 7.9-st protsendist liigume, seda enam see tõenäosus väheneb kuni selleni välja, et on täiesti ebatõenäoline, et tõeline toetusprotsent on kas 11% või 5%. 95% usaldusvahemiku piiridel see tõenäosus päris null ei ole (kuna 5% tõenäosusest jääb sellest usaldusvahemikust ju välja), kuid ta on üpriski madal. Ning ei pea nendest piiridest väga kaugele minema, et see tõenäosus jõuaks sisuliselt nulli. 

Kogu selle jutu moraal on see, et usaldusvahemik võib olla sama eksitav kui toetusprotsent ise, kui me selle omadusi ei teadvusta. Kui usaldusvahemik on 6.77 kuni 9.03 protsenti, siis ei tähenda see, et erakonna tegelik toetus võib sama hästi olla emb või kumb või mida iganes selle kahe piiri vahel. Kõige tõenäolisemalt on ta ikkagi see sama arv, mida oma andmetes näeme või midagi sellele suhteliselt lähedal. Mida kaugemale sellest keskpunktist liigume, seda ebatõenäolisem on, et tegelik toetus on just seal. 

See valearusaam – et usaldusvahemiku sees on iga väärtus samaväärne – viib edasi kahe teise eksimuseni, millele on samuti oluline tähelepanu juhtida. Need puudutavad toetusnumbrite võrdlemist. 

Oletame, et Isamaa, kelle toetus on 7.9%, kõrval on Sotsiaaldemokraadid, kelle toetus on 6.5%. Kui me need protsendid koos usaldusvahemikega joonisele kuvaksime, näeks see joonis välja selline.

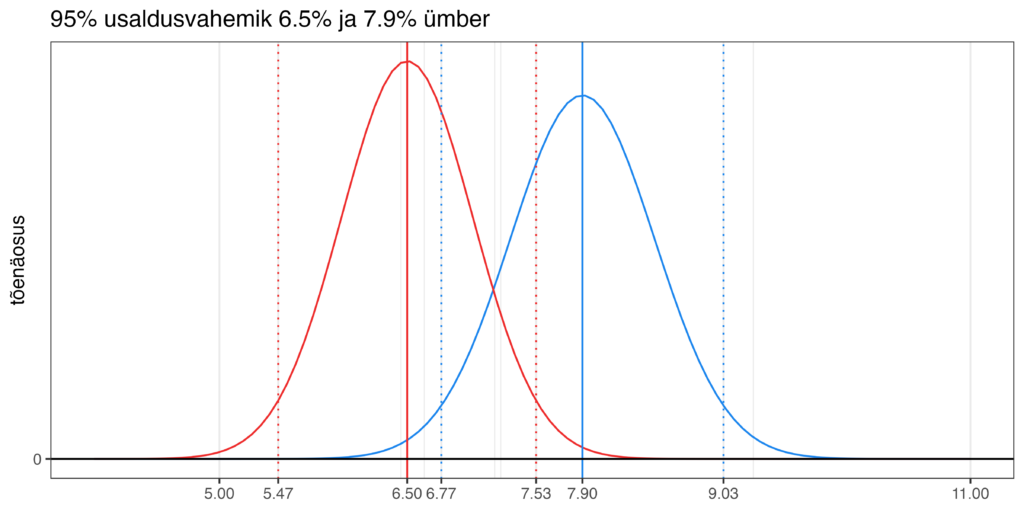
Usaldusvahemikud kattuvad siin päris suures ulatuses. Isamaa toetuse usaldusvahemiku alumine piir on 6.77 ja Sotside toetuse usaldusvahemiku ülemine piir on 7.53. Kui nüüd keegi, kes eeldab, et tõenäosus on usaldusvahemike sees ühtlaselt jaotunud, vaatab sellist olukorda, siis ta järeldab ilma suuremate probleemideta, et tegelikult võib nende kahe erakonna toetus olla sama. Et ei saa öelda, et ühe toetus on suurem kui teise. Tõde on aga see, et saab küll ning järeldus, et ühe toetus on suurem kui teise, on oluliselt tõesem, kui see, et nende toetus on võrdne või et hoopis Sotside toetus on suurem kui Isamaa oma.  

Me peame mõtlema tõenäosuslikult ja võtma arvesse vea tõenäosuse ebaühtlast jaotust usaldusvahemiku sees. Seda on aga intuitiivselt vägagi raske teha. Keeruline on hinnata, mis on see üldine tõenäosus, et Sotside tegelik toetus selle näite puhul on vähemalt sama suur, kui Isamaa toetus. 

Kuid teame selle tõenäosuskõvera omadusi ja kui natuke statistiliselt vaeva näha, siis saaksime ka oletada näiteks seda, et mis on see tegelik tõenäosus, et Isamaa toetus ei ole antud juhul suurem kui Sotside toetus. 

Oma andmetest me näeme, et Isamaa toetus on 7.9% ja Sotside toetus 6.5%. Muid andmeid meil ei ole ja kui me peaks midagi reaalsuse kohta järeldama, siis need kaks numbrit oleksid meie kõige paremad oletused. Kui eeldame, et need on tõesed numbrid – et tegelik toetus valijaskonnas on just nii suur – siis mis oleks see tõenäosus, et me oma juhuslikult eksivates andmetes näeksime vastupidist – et Isamaa toetus on tegelikult väiksem kui Sotside toetus?

Me võime antud juhul lasta arvutil seda tõenäosust hinnata, sellist olukorda simuleerida. Saame tulemuseks, et tõenäosus, et tegelikult on Sotside toetus vähemalt sama suur või suurem kui Isamaa toetus, on umbes 3.6%. See on päris väike. Ühesõnaga, kui taolise valimi suuruse (2200) puhul on kahe väikeerakonna toetuste vahe 1.4%, on tõenäosus, et see väljendab ka päriselt toetuste erinevust ühe erakonna kasuks, päris suur. Oleks äärmiselt eksitav väita, et nende kahe vahel tegelikult toetuste erinevust ei ole. 

See, et peab hindama ebaühtlaselt jaotunud tõenäosusi, maksab kätte, kui ei olda harjunud tõenäosustest mõtlema ja kui ei omata adekvaatset arusaama sellest, mida tähendab statistiline mõiste “usaldusvahemik”. 

Teine sarnane olukord, kus tõenäosusliku mõtlemise keerukus viib eksiteele, on siis, kui peame hindama, kas näiteks nädalast nädalasse toimunud muutused erakondade toetuses väljendavad tegelikku trendi või mitte. 

Tavaliselt muutuvad Norstati reitingutes toetused nädalast nädalasse väga vähe ning tüüpiline on olukord, kus ühel nädalal on erakonna toetus näiteks 9.8% ning järgmistel nädalatel näiteks 10.4%, siis 10.9% ja siis 11.5%. Nelja nädala jooksul on toetus muutunud väga väga ning kõik need arvud on sügavalt üksteise usaldusvahemike sees. Usaldusvahemikest ebaadekvaatse arusaamaga poliitikavaatlejale näeks see olukord välja selline.

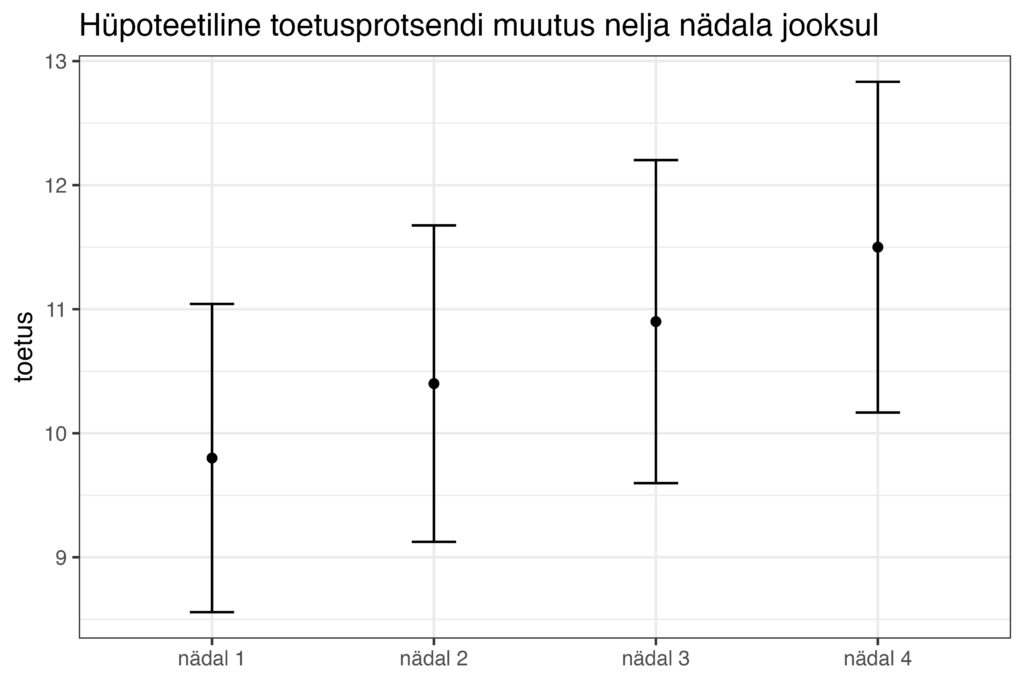
Reaalsuses on see pilt aga pigem selline.

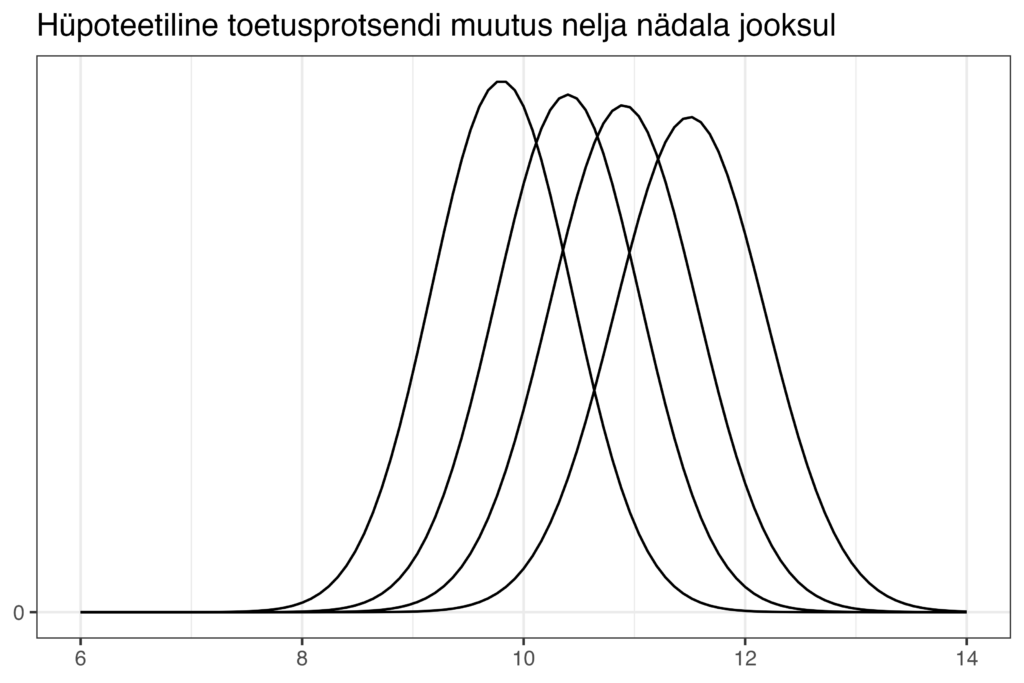
Nagu ka eelmise kahe toetusnumbriga näite puhul peame ka siin lisaks tõenäosuste ebaühtlasele jaotusele arvestama sellega, mis on see tõenäosus, et mitu asja juhtuvad korraga – antud juhul, et need kolm väikest toetuse muutust juhtuvad juhuslikult korraga samas suunas. Peame alustama selle hindamisega samamoodi nagu ka eelmise näite puhul. Eeldame, et reaalsuses just sellised väikesed muutused on toimunud. Mis oleks see tõenäosus, et statistilist viga arvesse võttes taolist kasvavat trendi ka oma andmetes näeme? Või kui suur on tõenäosus, et kui sellised väikesed muutused on tegelikult aset leidnud, meie juhuslikult eksivad andmed meile midagi muud näitavad? 

Me vaatleme nelja punkti ajas ning nende vahel võib olla kolm muutust. Me võime näha kolme kasvu; kahte kasvu ja ühte langust, ühte kasvu ja kahte langust või kolme langust. Kui päriselt on sellised väikesed muutused aset leidnud, siis mis antud juhul oleksid need tõenäosused?

See tõenäosus, et me ka oma andmetes näeme kolme järjestikust kasvu (et nädal kaks on suurem kui nädal üks, nädal kolm on suurem kui nädal kaks ja nädal neli on suurem kui nädal kolm), on umbes 30%. Selle tõenäosus, et me näeme kahte kasvu ja ühte langust (arvestades kõiki võimalikke kombinatsioone), on umbes 58%. Selle tõenäosus, et me näeme kahte langust ja ühte kasvu on umbes 12%. Ning see tõenäosus, et näeme kolme järjestikust langustrendi, on peaaegu olematu. Ehk siis kui päriselt on aset leidnud sellised väikesed muutused toetuses, siis see tõenäosus kokku, et me oma andmetes näeme kas kahe või kolme toetuskasvuga trendi, on umbes 88%. Kuigi kõik need usaldusvahemikud kattuvad, on ikkagi väga suur tõenäosus, et nende taga leiab päriselt aset mingi kasvutrend. 

Loodetavasti on nendest näidetest kasu toetusnumbrite ja usaldusvahemike tõlgendamisel. Tasub meeles pidada, et see number, mida oma andmetes näeme, on alati kõige tõenäolisem oletus selle kohta, mis võib päriselt tõene olla. Tõenäosus usaldusvahemike sees ei ole võrdselt jaotunud ning selle vahemiku äärealadel on see päris väike.